2. 疲劳寿命计算理论简介
Fatigue是用于结构疲劳寿命分析的程序,它是基于传统的疲劳寿命计算理论开发。
2.1 引言
美国材料与试验协会(American Society for Testing and Materials, ASTM)将疲劳寿命(Nf)定义为材料在发生特定的疲劳破坏前所经历的应力循环数。对于一些材料,例如钢和钛,存在一个理论应力值(SNf),当应力小于SNf,材料可以承受无限次数的应力循环,该应力值通常被称为疲劳极限或疲劳强度。
工程上常用的材料疲劳寿命预测方法有:
- 应力-寿命方法
- 应变-寿命方法
- 裂纹扩展方法
- 基于寿命或裂纹扩展的随机概率方法
不管采用上面哪一种预测方法,结构所受的复杂变化载荷最后一般都采用雨流计数等技术手段将其转换成等效的简单加载情况来处理。Fatigue目前主要采用的是应力-寿命计算方法,由于其它计算方法的基本流程和技术手段类似,后期将继续扩展Fatigue,增加其计算功能。
该部分内容的理论参考资料:
- [1] https://en.wikipedia.org/wiki/Fatigue_(material)
- [2] Schijve J., Fatigue of structures and materials, 2nd ed., Springer, 2009.
- [3] Dowling, Mean Stress Effect in Stress-Life and Strain-Life Fatigue. In: SAE Paper No. 2004-01-2227, 2004.
2.2 疲劳载荷类型与基本术语
使零件或构件发生疲劳破坏的动载荷称为疲劳载荷,可分为为两类:一类是其大小和正负方向随时间周期性地变化的交变载荷,另一类是大小和正负方向随时间随机变化的随机载荷。交变载荷又称为循环载荷,是最为简单和基本的疲劳载荷形式。所研究结构部位因交变载荷引起的应力称为交变应力。
图 2.1 对称循环交变载荷
图 2.1是一个典型的交变应力一时间的变化历程。图中循环应力的大小和正负方(拉压)向随着时间的变化而作周期性的变化。一个周期的应力变化过程称为一个应力循环。应力循环特点可用循环中的最大应力σmax、最小应力σmin和周期来描述。因为最大应力和最小应力的绝对值相等而正负号相反,故称这种交变载荷为对称循环应力。典型的循环载荷如圆轴类杆件的旋转弯曲、轴向拉压和平板零件的双向弯曲等,都可以在零件的表面或内部产生这样的交变应力。另外,轴类零件的双向扭转也可以产生类似的交变应力。
在疲劳载荷的描述中经常使用应力幅σa。和应力范围Δσ。(也称为应力振幅、应力幅度)的概念,定义如下: $$ \sigma_a=\frac{\sigma_{max}-\sigma_{min}}{2} $$ 应力幅σa反映了交变应力在一个应力循环中变化大小的程度,它是使金属构件发生疲劳的根本原因。
当研究的部位除承受有动载荷外,还有静载分量荷时,动静载荷的共同作用下的应力-时间变化曲线如图2.2所示。
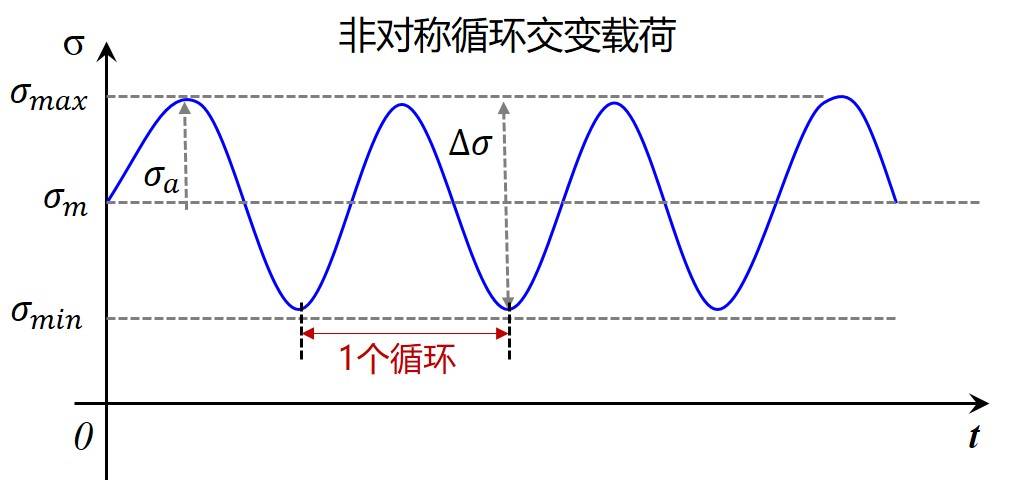
图 2.2 非对称循环交变载荷
此时的载荷时间-变化曲线相当于把图2.1的对称循环应力曲线向上平移一个了静应力分量。这种循环载荷称为非对称循环载荷,并用最小应力与最大应力的比值R来描述循环应力的不对称程度,R称为应力比,有时又称为不对称系数,即: $$ R=\frac{\sigma_{min}}{\sigma_{max}} $$ 由定义可知,当R=−1时的循环应力即为对称循环应力,当R≠0时统称不对称循环应力。其中,R=0时为拉伸脉动应力,R=−∞为压缩脉动循环。循环应力中的静载分量通常称为平均应力,用σm表示,可由下式求出: $$ \sigma_m=\frac{\sigma_{max}+\sigma_{min}}{2} $$ 静载分量或平均应力对构件的疲劳强度有一定的影响。压缩平均应力往往提高构件的疲劳强度,拉伸平均应力往往降低构件的疲劳强度。因此,在疲劳强度和疲劳寿命的研究中, 给定一个循环应力水平时,需要同时给出应力幅σa和应力比R、或者同时给出最大应力σmax和平均应力σm,也有时直接给出最大应力σmax和最小应力σmin来表示循环应力水平。
由以上各式可知,在应力幅、平均应力、应力比、最大应力和最小应力的参数中,只要已知其中的两个便可求出其它。
2.3 材料的S-N曲线与基本术语
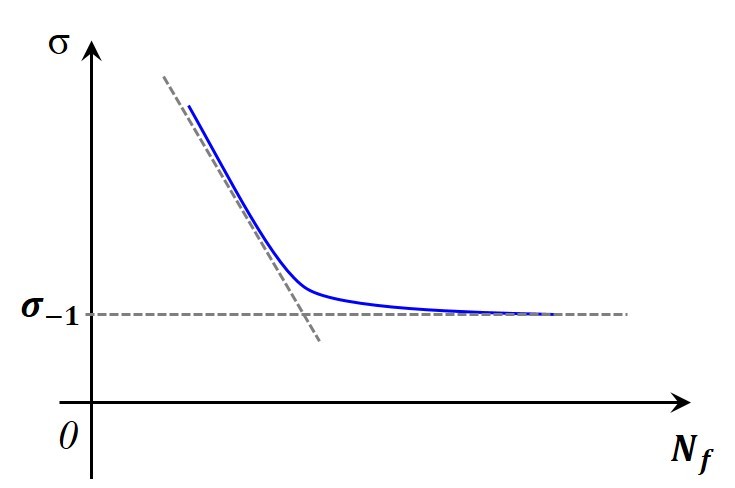
一般情况下,材料所承受的循环载荷的应力幅越小,到发生疲劳破断时所经历的应力循环次数越长。S-N曲线就是材料所承受的应力幅水平与该应力幅下发生疲劳破坏时所经历的应力循环次数的关系曲线。S-N曲线一般是使用标准试样进行疲劳试验获得的。如图2.3所示,纵坐标表示试样承受的应力幅,有时也表示为最大应力,但二者一般都用$\sigma$表示;横坐标表示应力循环次数,常用$N_f$表示。为使用方便,在双对数坐标系下S-N曲线被近似简化成两条直线。但也有很多情况只对横坐标取对数,此时也常把S-N曲线近似简化成两条直线。
图 2.3 S-N曲线
S-N曲线中的水平直线部分对应的应力水平就是材料的疲劳极限,其原意为材料经受无数次应力循环都不发生破坏的应力极限,对钢铁材料此“无限”的定义一般为$10^7$次应力循环。但现代高速疲劳试验机的研究成果表明,即使应力循环次数超过$10^7$材料仍然有可能发生疲劳断裂。不过$10^7$次的应力循环次数,对于实际的工程中的疲劳强度设计已经完全能够满足需要。疲劳极限又称持久极限,对于无缺口的光滑试样,多用$\sigma_{w0}$表示,而应力比$R=-1$时的疲劳极限常用$\sigma_{-1}$来表示。某些不锈钢和有色金属的S-N中没有水平直线部分,此时的疲劳极限都一般定义为$10^8$次应力循环下对应的应力幅水平。疲劳极限是材料抗疲劳能力的重要性能指标,也是进行疲劳强度的无限寿命设计的主要依据。
计算中的S-N曲线参数
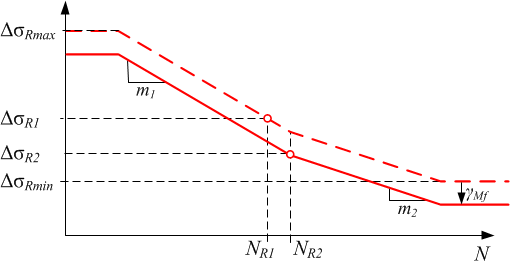
在实际Fatigue计算中,会用如图2.4中的参数来定义SN曲线。其中红色的虚线是用户输入的实际SN曲线,而红色实线表示计算中实际用到的SN曲线。虚线和实线的区别在于,实线在虚线的基础上加了一个安全系数($\gamma_{Mf}$),导致实线相对于虚线向下有一个平移量,但两条曲线的直线段曲率是一样的。为便于计算,材料的疲劳性能SN曲线可拟合成图中的形式,计算中需要给定的参数包括,两个斜线段的斜率m1和m2,疲劳强度$\Delta\sigma_{R1}$,疲劳强度对应的循环次数$N_{R1}$,以及通过安全系数修正后的拐点循环次数$N_{R2}$。另外,可以定义SN曲线的应力截断范围$\Delta\sigma_{Rmin}$和$\Delta\sigma_{Rmax}$,低于$\Delta\sigma_{Rmin}$的应力水平将被忽略掉,应力水平高于$\Delta\sigma_{Rmax}$时,损伤将设置为$D\ge1$。其中$\Delta\sigma_{R2}$可通过其它参数计算得到,不需要给定。这些参数可以通过SN曲线文件格式提交到Fatigue程序进行分析。
图 2.4 计算用到的S-N曲线参数定义
2.4 平均应力修正
产生疲劳破坏的根本原因是动应力分量,但静应力分量即平均应力对疲劳极限也有一定的影响。在一定的静应力范围内,压缩的静应力提高疲劳极限,拉伸的静应力降低疲劳极限。一般认为,残余应力对疲劳极限的作用同平均应力的作用相同。对一种材料,可根据它在各种平均应力或应力比$R$下的疲劳极限结果画出疲劳极限图。
平均应力的影响可以通过不同的方式来对SN曲线进行修改,修正的方式和参数可以通过材料疲劳参数文件来指定。如果定义$\sigma_{a,-1}$为对称循环应力下应力幅值,平均应力为$\sigma_m$,应力比为$R$,通过平均应力修正后的应力幅值为$\sigma_{a,R}$,那么可以通过不同方式来确定$\sigma_{R,-1}$来用于疲劳寿命的计算。Fatigue中支持的平均应力修正方式有:不修正、线性修正、双线性修正、Modified Goodman修正、Soderberg修正、Gerber parabola修正、Smith-Watson-Topper修正、60%压缩准则、IIW中低残余应力修正、FKM参考线修正。下面是各种修正形式的公式和参数说明。
不修正
即不对平均应力进行修正处理。对于一些焊接或铆钉连接推荐采用这种方式,因为平均应力效应已经包含在相应的SN曲线中了。
线性修正
线性修正的关系式为: $$ \sigma_{a,R}=\sigma_{a,-1}-M\sigma_{m} $$ 其中$M$为平均应力灵敏度,可能通过实验数据得到,定义为: $$ M=\frac{\sigma_{a,-1}}{\sigma_{a,0}}-1 $$ 其中$\sigma_{a,0}$是$R=0$时的疲劳强度,$M$值的范围一般为0.2到0.4。
双线性修正
当$R<0$时,双线性修正与线性修正是一样的。当$R>0$时,它的修正方式与Goodman修正类似,具体形式为: $$ {\sigma_{a,R}} = \left\{ \begin{array}{l} {\sigma_{a, - 1}} - M{\sigma_m}, {\sigma_m} \le {\sigma_{a,0}} \\ \frac {\sigma_{a,0}(\sigma_u - \sigma_m)} {\sigma_u - \sigma_{a,0}}, {\sigma_m} > \sigma_{a,0} \end{array} \right. $$ 其中$\sigma_{a,0}=\frac{\sigma_{a,-1}}{M+1}$,$\sigma_u$为拉伸强度极限。
Modified Goodman修正
Modified Goodman修正的关系式为: $$ \sigma_{a,R}=\sigma_{a,-1}(1-\frac{\sigma_{m}}{\sigma_u}) $$ 对于一些高强度或者低韧性的材料推荐采用这种修正方式。
Soderberg修正
Soderberg修正的关系式为: $$ \sigma_{a,R}=\sigma_{a,-1}(1-\frac{\sigma_{m}}{\sigma_y}) $$ 其中$\sigma_y$屈服极限。
Gerber parabola修正
Gerber parabola修正与Modified Goodman修正类似,只是第二项采用的是平方形式: $$ \sigma_{a,R}=\sigma_{a,-1}(1-\frac{\sigma _m^2}{\sigma _u^2}) $$
Smith-Watson-Topper修正
Smith、Watson和Topper所定义的修正关系式为: $$ \sigma_{a,R}=-\frac {1}{2} \left( {\sigma _m} - \sqrt {\sigma _m^2 + 4 \sigma _{a, - 1}^2} \right) $$ 这一修正只适用于拉伸区域。
60%压缩准则
在有的程序中允许只使用压缩部分应力来做修正:
其中$\sigma_{c,R}=\sigma_{a,-1}/0.6$是压缩载荷下获得的最大疲劳强度。
IIW中/低残余应力修正
根据残余应力值的大小,对压缩载荷下的疲劳强度进行一定的放大:
- 低等残余应力:放大值为1.6
- 中等残余应力:放大值为1.3
- 高等残余应力:不放大
采用该方法,请参考:Hobbacher A., IIW recommendations for fatigue design of welded joints and components, IIW-doc. XIII-2460-13, 2013.
FKM参考线修正
根据FKM参考线,平均应力修正分为4个区域:
其中$\sigma_{a, - \infty } = \frac{ \sigma_a} {1 - M}$,$\sigma_{a,0} = \frac{M + 3} {M + 1}$。
采用该方法,请参考: FKM-Richtlinie: Rechnerischer Festigkeitsnachweis für Maschinenbauteile aus Stahl, Eisenguß- und Aluminiumwerkstoffe, 4. Ausgabe. VDMA-Verlag, Frankfurt/M. 2002
2.5 应力时间历程
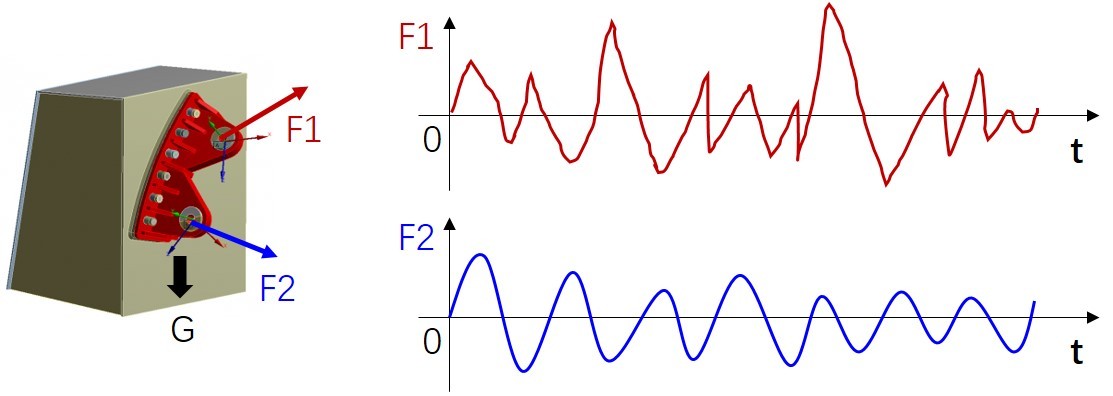
结构的疲劳是由于动载荷的作用导致的,但一个结构在服役过程中可能同时受多个复杂载荷的作用。如图2.5所示结构,该结构同时受重力、F1、F2的作用。重力是不随时间变化的,而F1、F2是随时间变化的。为了获得结构在当前工况下每个位置的应力历程,需要开展有限元计算。计算的方式一般有两种:
- 直接法:直接用有限元计算结构在所有载荷下的动力学响应,并获得每个时间点结构的应力分布。
- 叠加法:根据叠加法则,可以先用有限元静力学计算每个载荷工况下对应单位载荷时的应力分布,再将各个载荷的时间历程与单位载荷应力分布相乘,最后对所有工况应力相加就可以得到复杂工况下的应力历程。
图2.5 同时受重力、F1、F2作用的结构
采用直接法计算的应力历程是最精确的,但其计算量大。而且当结构的单元数目较多,计算时间步较长时,需要存储巨大的应力历程数据。所以,实际计算中采用叠加法。
在叠加法中,可以根据载荷特征分成几个独立的载荷工况(Load Cases)。例如,图2.5中有3个载荷工况:重力(G)、F1和F2。如果在真实情况中,F1和F2的载荷历程是完全一致的,可以将F1+F2合并为一个载荷工况。
若一个结构同时受到N个载荷工况,基对应的载荷历程为$F_i(t)$,采用叠加法计算结构的应力时间历程时,首先,针对每一个载荷,在其加载位置施加单位载荷$f_i^1$,计算得到在该单位载荷作用下结构的应力分布$\sigma_i^1$。则结构在所有载荷工况下的应力时间历程可以通过叠加得到: $$ \sigma (t) = \sum {\sigma _i^1{F_i}(t)} $$ 叠加法只需要计算和存储每个载荷工况单位载荷下的应力分布即可,而载荷时间历程$F_i(t)$可根据实际情况变化,因此其计算量和存储量更加小,更加灵活。但叠加法的前提是各个载荷工况得到的单位载荷应力分布是可以叠加的,但对于一些非线性材料或结构响应而言,这一条件不一定能得到满足。例如,如果材料是拉压不对称的,当$F_i(t)$为正时,应力如果为$\sigma _i^1{F_i}(t)$;但当$F_i(t)$为负时,其应力结果可能变化为$c\sigma _i^1{F_i}(t)$。另外,也存在不同载荷之间需要进行非线性叠加的情况,针对这些非线性叠加的要求,可以通过不同的非线性模型来近似处理。Fatigue中支持的非线性叠加方式有双线性叠加、一维插值、二维插值,如图2.6所示。
图2.6 非线性叠加方式
双线性叠加
为进行双线性叠加,需要先计算结构分别在单位载荷为正和为负的情况下的应力分布,然后判断载荷在不同时间步的正负情况,采用不同的应力分布进行计算。
一维插值
当分析的问题是大变形问题,或者材料的非线性响应很强是时,可以采用一维插值方式。采用一维插值时,需要提前计算结构在几个插值点载荷作用下的应力分布,然后再根据真实载荷所处的区间来插值得到对应的应力分布。
二维插值
与一维插值类似,如果应力分布是与2个参数相关的,需要提前计算结构在几个二维插值点载荷作用下的应力分布,然后再根据真实载荷所处的区间来插值得到对应的应力分布。
2.6 疲劳应力计算
在运用SN曲线进行疲劳分析时,计算所需要的应力幅值$\sigma_a$、平均应力$\sigma_m$都是标量。但应力时间历程计算得到的应力是一个张量,因此需要基于应力张量计算一个标量值,用于疲劳应力分析。计算得到的这个标量值称为疲劳应力,根据材料和结构的不同,疲劳应力的计算方式也有所不同。常用的疲劳应力计算方法有:Von Mises应力、含符号的Von Mises应力、主应力、最大拉应力、最大剪应力等。
Von Mises应力
Von Mises应力的计算公式为: $$ \sigma_{vm}=\sqrt {\frac {1}{2}((\sigma_x-\sigma_y)^2+(\sigma_y-\sigma_z)^2+(\sigma_z-\sigma_x)^2+6(\tau_{xy}^2+\tau_{yz}^2+\tau_{xz}^2))} $$ 如果采用含符号的Von Mises应力: $$ \sigma_{svm}=sign(\sigma_x+\sigma_y+\sigma_z) \cdot \sigma_{vm} $$
主应力
应力张量的三个主应力可以通过求解其特征值获得:$\boldsymbol{\sigma}_p=eig(\sigma(t))$,按照大小有:$\sigma_1>\sigma_2>\sigma_3$。在疲劳应力计算中,可以选取不同的主应力作为疲劳应力。通常选取数值最大的主应力$\sigma_{pnmax}$,这也是疲劳应力计算中默认方式: $$ \sigma_{pnmax}=\left\{ \begin{array}{l} \sigma_1, for \left| \sigma_1 \right| \ge \left| \sigma_3 \right| \\ \sigma_2, for \left| \sigma_3 \right| < \left| \sigma_3 \right| \end{array} \right. $$
临界面分析
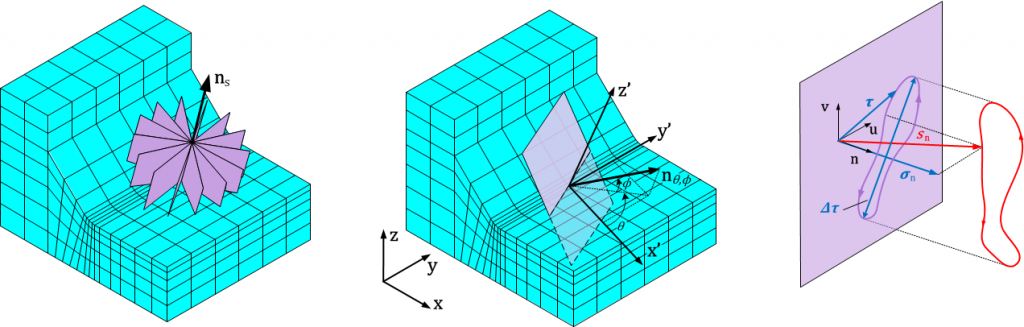
临界损伤平面法它考虑了应力应变张量,以顾及到应力应变张量时程,并以此确定其最大损伤平面。临界损伤平面法适用于对比例及非比例两种加载情形进行寿命计算,反映了多轴疲劳危险面的物理意义。临界面方法是找出最有可能发生裂纹的平面,判断裂纹发生可能性采用的是损伤参数。在对结构表面某一点的应力做临界面分析时,会寻找该点处不同平面的损伤参数值,其中损伤参数值最大的平面称为临界平面。但实际计算中不可能遍历所有的平面,只能取有限个平面进行分析,因此需要用户指定平面数目。程序会根据平面数,构造在空间均匀分布的平面集,然后在每个平面上计算损伤参数值,最后确定出面最大损伤的平面作为临界面,以临界面上的应力作为疲劳应力进行下一步的求解。
图2.7 临界面分析
为了进行临界面分析,人们定义了多种损伤参数,常用的有正应力准则、IIW等效应力、Findley准则等,目前Fatigue支持正应力准则的临界面分析,它常用于半韧性的材料,其定义为: $$ \Delta \sigma_{CP-N} = \mathop {\max } \limits_{0 \leqslant \theta \leqslant \pi } \Delta {\sigma _n} $$ 在单轴加载时,正应力准则与主应力准则是相对应的。但在非单轴加载时,采用正应力准则避免了不同方向上的损伤累积计算。
2.7 循环计数
结构在实际工况下承受的交变载荷其载荷幅值往往是不规则变化的,称为变幅载荷或不规则载荷。为了能应用S一N曲线和累计损伤理论进行疲劳分析,首先要把实测载荷历史简化为等效的由恒幅载荷块组成的载荷谱,这类处理方法称为“循环计数方法”(简称“计数法”)。循环计数是对疲劳应力历程与标准应力循环相连接的一个操作。目前Fatigue支持的循环计数方式包括:
- 蓄水池法(默认方法)
- 雨流计数法(全循环和半循环)
- 雨流计数法(全循环)
不同方法的操作过程可参考:陆明万, 寿比南, 杨国义. 疲劳分析中变幅载荷的循环计数方法. 压力容器, 9(11), 2012
2.8 累积损伤
1924年,Palmgren在估算滚动轴承的寿命时,假设损伤累积与转动次数成线性关系,首先提出疲劳损伤的累积为线性的假设。1945年,Miner结合铝合金的疲劳累积损伤问题,提出了相同的假设并将其公式化,形成著名Palmgren-Miner线性累积损伤准则。Fatigue中也是采用的Palmgren-Miner线性累积损伤准则。
对于一个给定的应力水平$\Delta\sigma_i$,经过循环计数得到其循环次数为$n_i$,而根据SN曲线,在当前应力水平下对应的循环次数为$N_i$,那么根据Palmgren-Miner线性累积损伤准则,结构在所有应力水平循环下的损伤为: $$ D = \sum\limits_i^q {\frac{{{n_i}}}{{{N_i}}}} \leqslant {D_{al}} $$ 当累积损伤$D=1.0$时,认为结构发生了疲劳破坏。但实际的损伤值变化范围很大(在0.1-10)之间变化,因此,不同软件对于发生疲劳破坏的损伤值不一样。
2.9 疲劳计算结果
在Fatigue的计算结果输出中,除了上面所提到的累积损伤之外,还有一些其它物理量可以用于疲劳寿命分析和判断。
疲劳寿命
疲劳寿命通过疲劳损伤和施加载荷循环次数计算得到: $$ N_{life}=\frac {N_{applied}} {D} $$ 它是结构疲劳寿命最直接的反映,表示在当前加载条件下,结构各表面结点处可承受的循环次数,一般它的值比较大,在云图时建议取对数再作图。
等效损伤应力水平
对照S-N曲线中双斜线段的不同斜率,等效损伤应力水平的计算公式为: $$ \Delta {\sigma_{eq}} = {\left( {\frac{1}{{{D_{al}}}}\frac{{\sum {{n_i}\Delta \sigma_{i,{\sigma_m} = 0}^{m1}} + \sigma_{R1}^{m1 - m2} \cdot \sum {{n_j}\Delta \sigma_{j,{\sigma_m} = 0}^{m2}} }}{{\sum {{n_i}} + \sum {{n_j}} }}} \right)^{1/{m_1}}} $$ 式中的$i$和$j$分别表示处于SN曲线中的$m1$和$m2$段。容许损伤$D_{al}$默认为1.0。但在SN曲线输入文件中可以改变。
它代表的是在当前的加载循环条件下,相当于S-N曲线中何等应力水平。
利用率 (Utilization Ratio)
利用率的计算公式为: $$ UR = \frac{{\Delta {\sigma _{eq}}}}{{\Delta {\sigma _{R2}}}} $$ 即等效损伤应力水平与S-N曲线中拐点处应力水平的比值,用于判断材料在这一点的疲劳利用率。


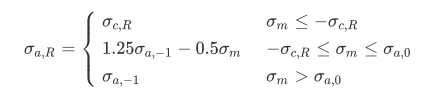
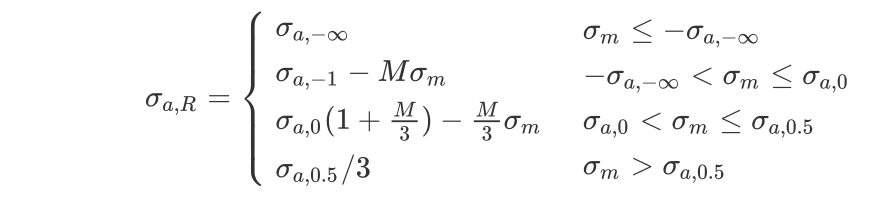

No Comments